Project 2: Filter (Algo)

You can find the handout for this project here. Please read the handout before working on this algo assignment!

Convolution

Discrete Convolution

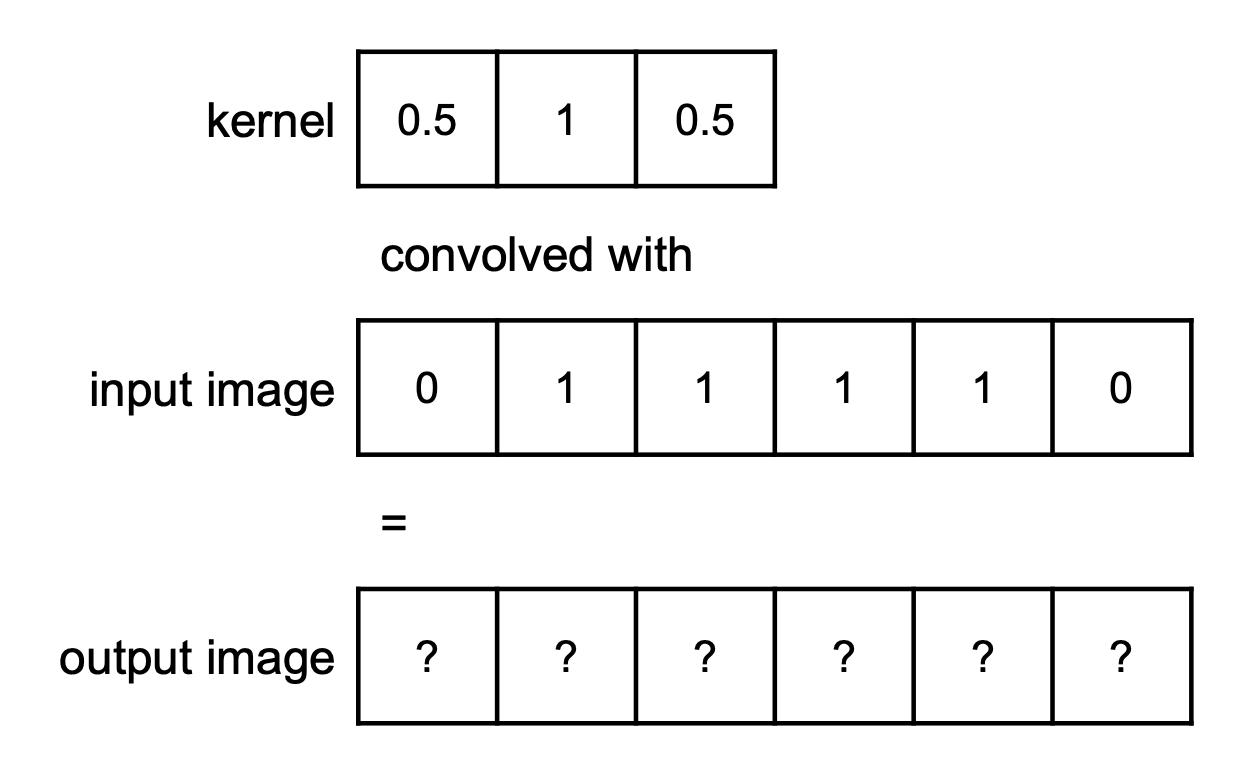
You are given the following 1D kernel and input image. Assume that any pixel outside the bounds of the input image has value 0 (i.e. the image is zero-padded).

What is the output image when the kernel and image are convolved with each other? Present your answer as a vector of size 6, representing the output image.

**Figure 1:** 1D arrays representing the input image, kernel, and output image (unfilled).

Continuous Convolution

Convolve the below function and filter. What is the value of at in the output?

TODO — **Figure 2:** Image as a continuous signal with filter function for Q1.2

Visualizing Convolution

Draw the shape of the output function obtained in the previous question (figure 2).

Blurring

Let's try to generalize our solution to the earlier discrete convolution problem.

Consider a 1D kernel of radius that represents a blurring filter. We apply this blur (via convolution) to an input image resulting in a new image .

All of , , and can be considered as 1D arrays storing intensities where gives the intensity of the -th pixel. Remember that the kernel is zero-indexed so gives the left-most value in the kernel array.

We are interested in writing out this convolution as summation over the values of and . For some index within the bounds of the image, please write out the summation equation for in terms of , , , and .

You may ignore edge effects for the purposes of this question (i.e. feel free to "incorrectly" index out-of-bounds).

Scaling

Scaling Up

What is the filter support width when you scale by a factor of , where ?

Scaling Down

What is the filter support width when you scale by a factor of , where ?

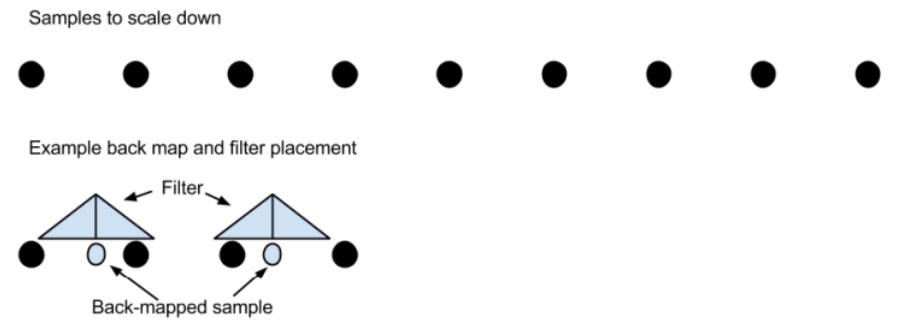
Naïve Back-mapping

Recall that back-mapping refers to finding the correct filter placement given a pixel in the output image.

The naïve back-map function is $ï$ , but the correct back-map function is .

Suppose we wanted to scale down a 9-pixel 1D image by a factor of ().

Draw a picture to show where we would sample the original image using the naïve back-map function. Please include an illustration of the filter above each sample point.

Correct Back-map

Draw another picture to show where we would sample the original image using the correct back-map function. Again, please include an illustration of the filter above each sample point.

Duality of Domains

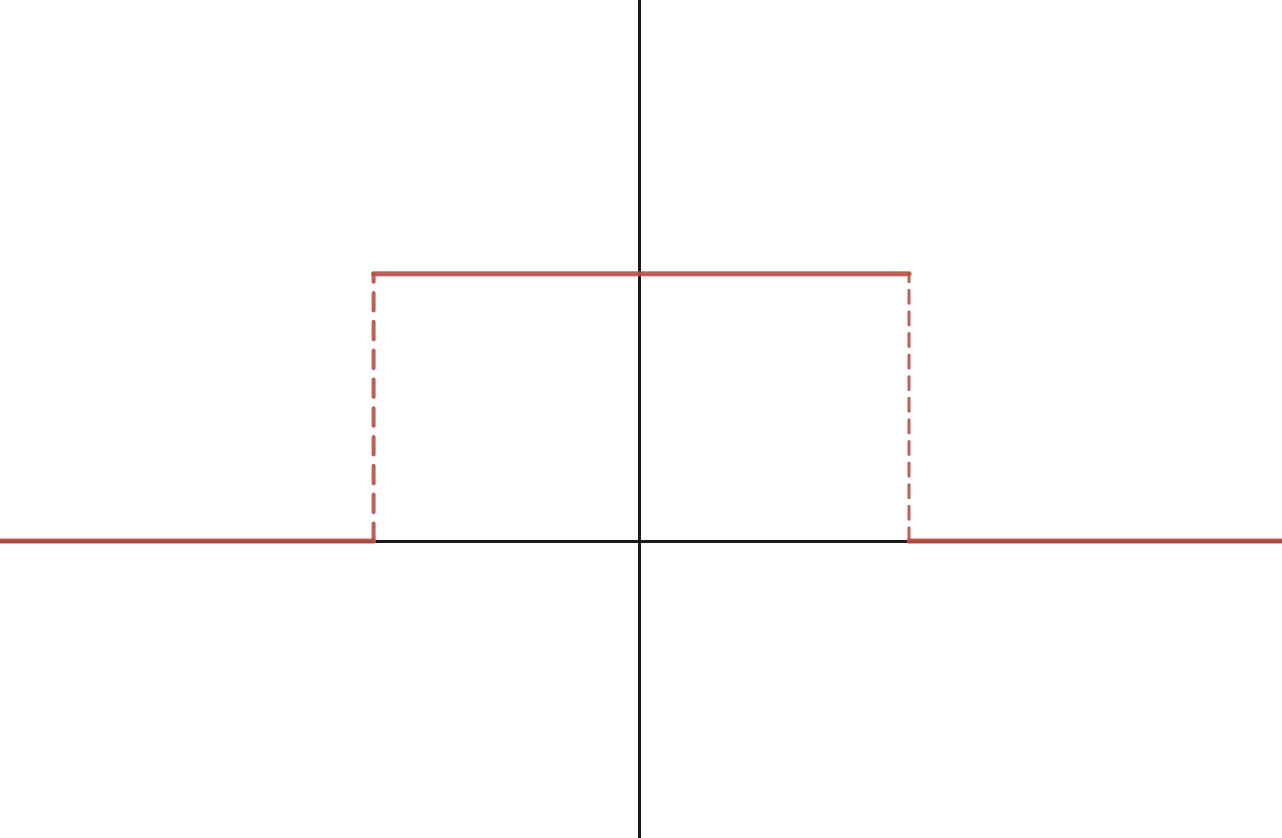
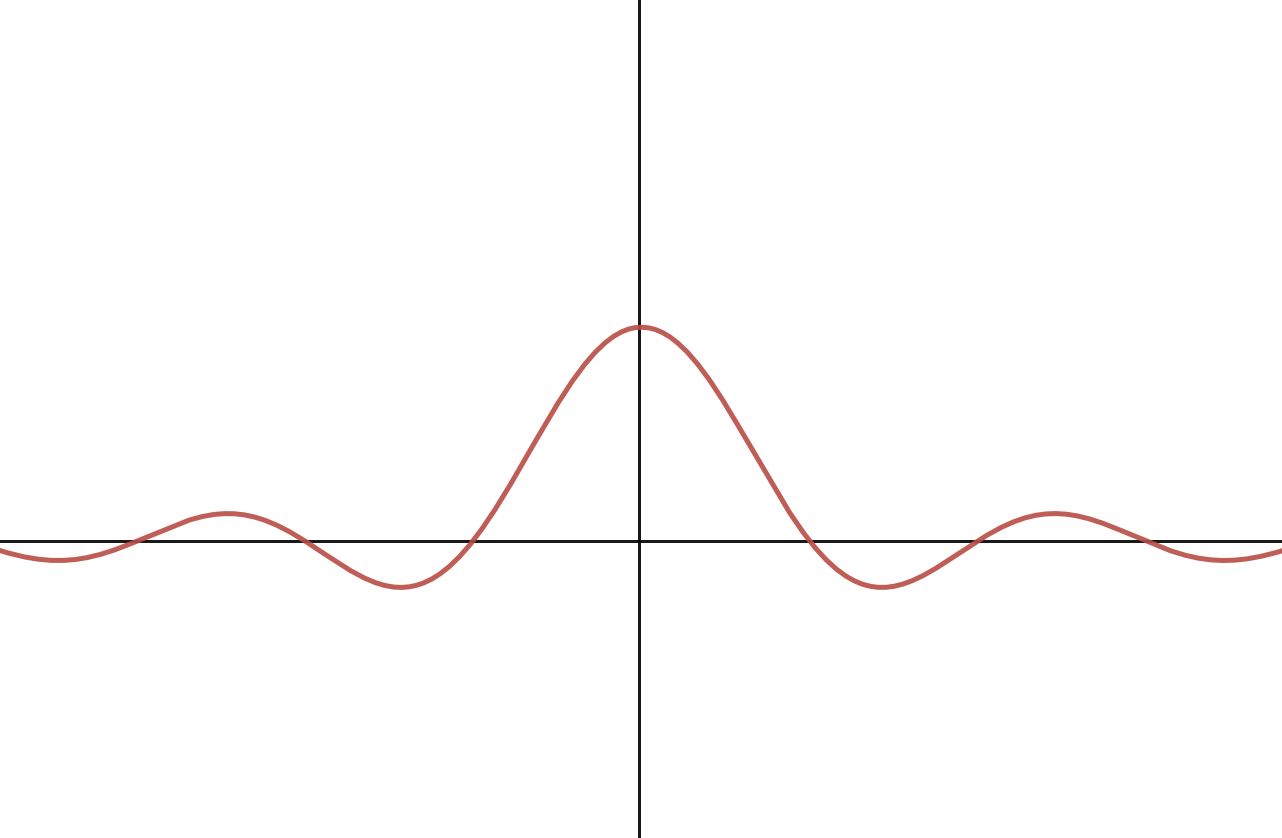
Visualizing Sinc and Box Duals

Take a look at the box function in figure 4 (left) below. Its dual in the frequency domain is the sinc function, in figure 4 (right). Note that there are no labels on the axes, by design.

**Figure 4:** A box function with its dual, a sinc function.

A sinc function — **Figure 4:** A box function with its dual, a sinc function.

Please sketch the dual of the box function in figure 5. Your drawing doesn't need to be perfectly accurate; we just need to see that you get the idea.

**Figure 5:** Another box function, about twice as wide as before.

Approximating Sinc

What do we usually use to approximate the sinc function, and why do we have to make this approximation when translating these theoretical concepts into code?

Sampling in the Frequency Domain

If we're sampling a continuous function at a frequency of samples per unit, what is the largest frequency we can represent, according to the Nyquist limit?

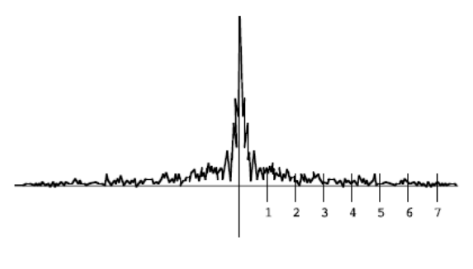
Frequency Plots

Now, examine the following frequency plot of a 1D, continuous signal. If you were going to sample this signal at a rate of 8 samples per unit, to avoid aliasing, you would use what we know about the Nyquist limit to pre-filter it. Sketch the new frequency plot after someone has performed this pre-filtering step optimally.

Submission

Submit your answers to these questions to the "Project 2: Filter (Algo)" assignment on Gradescope.