Project 5: Lights, Camera (Algo)
You can find the handout for this project here.
Projection Matrices
In lecture, we learned the two matrices that describe the camera: view and projection. In Ray, you learned how to generate a view matrix from a position, look, and up vector. In the Realtime projects, you will explore the concept of a projection matrix which covers the geometry of a view frustum!
Visuals
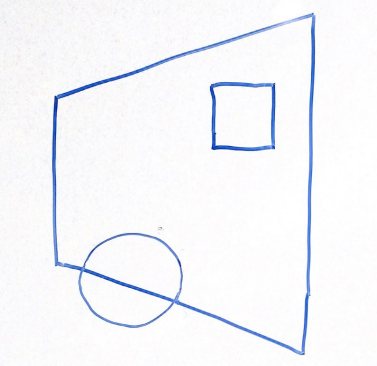
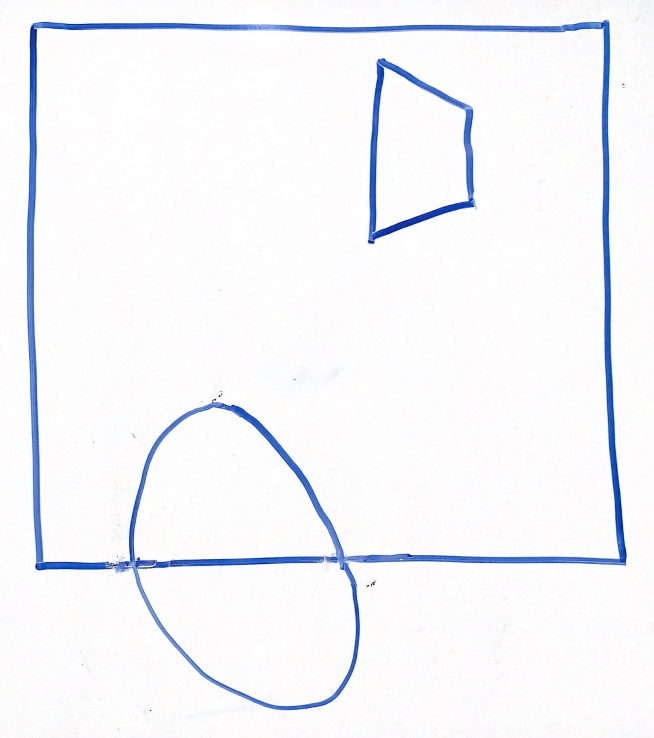
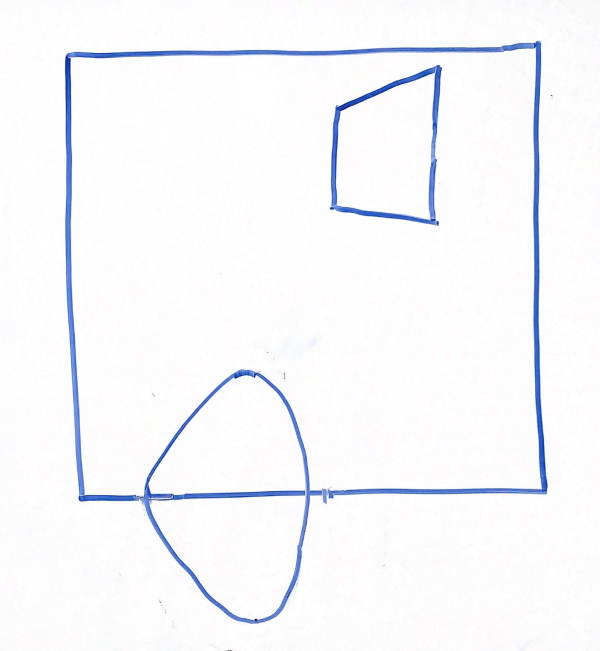
For the above scene in a 2D frustum, which of the following options best represents the same scene after being projected into clip space via a perspective projection?
Option 1 | Option 2 |
|---|---|
 |  |
Option 3 | Option 4 |
|---|---|
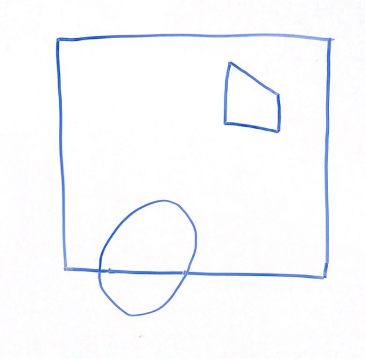 | 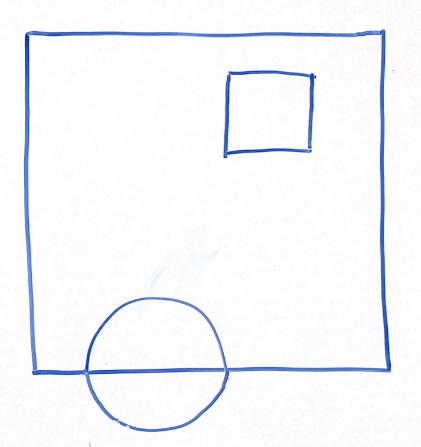 |
Scaling
Given a far plane distance of 100, height angle of 60 degrees, and a width angle of 90 degrees, what would the scaling matrix look like? Refer to this lecture for a reminder.
Unhinging
Given a near plane distance of 0.1 and a far plane distance of 100, what would the parallelization matrix look like? Refer to this lecture for a reminder.
Converting to OpenGL Space
The matrix below is multiplied on the left side of the two matries above to convert to OpenGL's expected space. What are the x, y, and z limits in OpenGL's clip space and what is this doing to our previous projection to convert it to these limits?
Vertex Attributes
Vertex Buffer Format
Using
Vertex Arrays
For each attribute above (position, color, and texture coordinate), please provide the stride and offset (pointer) in bytes using size_of(GLfloat). (Assume GL_FLOAT)
| Stride | Offset | |
|---|---|---|
| Position | ||
| Color | ||
| Texture Coordinates |
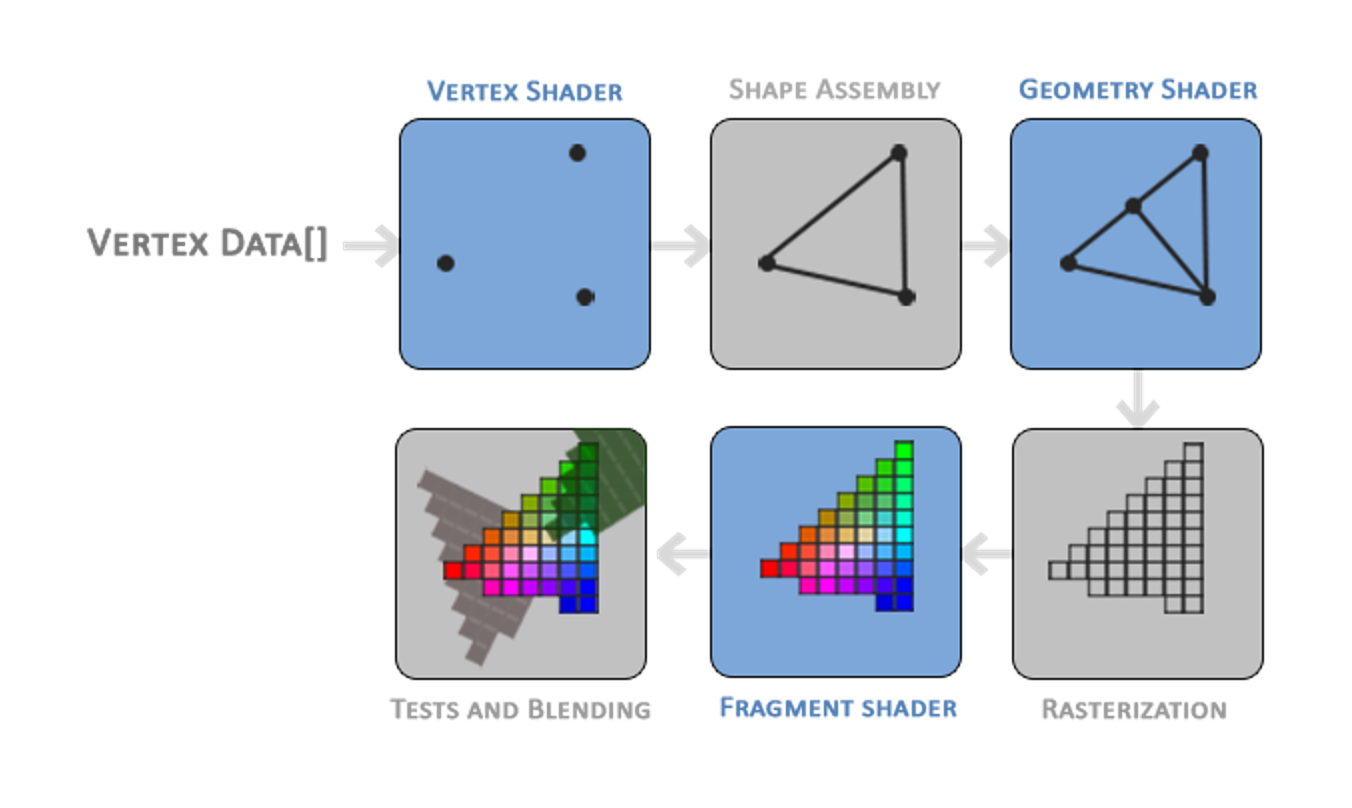
Realtime Pipeline
Rasterization
What does rasterization do? How does rasterization fit into the realtime pipeline in terms of inputs and outputs?
Shader Programs
We can perform the same types of computation in both fragment and vertex shader. For this problem, compare the performance considerations associated with applying coordinate transforms in the vertex shader vs. the in fragment shader.
If we are drawing 1 triangle which covers exactly 50% of the pixels on an 1280 x 720 image, is it more efficient to compute an operation in the vertex shader or the fragment shader, why, and by how much so?
In addition, please give an example of a computation that must be performed in the fragment shader.
Program Analysis
Erroneous Code
Consider the following initializeGL pseudo-code:
create VBO
bind VBO
fill VBO with data
unbind VBO
create VAO
bind VAO
set VAO attributes
unbind VAO
What would be the issue if a student tries calling glDrawArrays to draw their VAO in paintGL?
How could you change this pseudo-code to remove the error?
Predict the Render
Given a VBO filled with data from an std::vector<GLfloat> of size 18, and VAO attribute code of:
glEnableVertexAttribArray(0);
glEnableVertexAttribArray(1);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(GLfloat), nullptr);
glVertexAttribPointer(1, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(GLfloat), reinterpret_cast<void *>(3 * sizeof(GLfloat)));
How many vertices and how many triangles are described in the VBO/VAO pair?
If the VAO attribute code was changed to:
glEnableVertexAttribArray(0);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 3 * sizeof(GLfloat), nullptr);
How many vertices and how many triangles are now described in the VBO/VAO pair?
Submission
Submit your answers to these questions to the "Algo 5: Lights, Camera" assignment on Gradescope. Instructions on using Gradescope are available here.